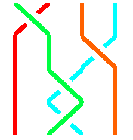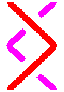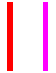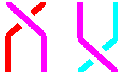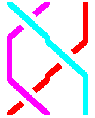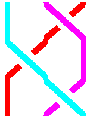Tresses isotopes.
Deux tresses sont isotopes si l'on peut passer de l'une à l'autre
sans détacher les extrémités des brins ni en haut
ni en bas de la tresse. On ne peut pas non plus briser les brins, c'est
à dire que deux brins ne peuvent pas se traverser.
Deux exemples de tresses isotopes.
-
Premier exemple :
L'ordre des deux premiers croisements s'inverse et les deux derniers croisements
s'annulent l'un avec l'autre.
-
Deuxième exemple :
La tresse de droite est la même que celle de gauche. En effet, pour
les deux tresses on a :
-
Le brin vert est situé au dessus des autres et il part de la première
position pour arriver à la seconde.
-
Le brin bleu est entre le vert et le rouge et il part de la deuxième
position pour arriver a la troisième.
-
Le brin rouge est au dessous des autres et il part de la troisième
position pour arriver a la première.
L'isotopie et les mots.
Il est possible de savoir a partir de l'ecriture sous forme de mots de
deux tresses si elles sont isotopes. Les tresses seront isotopes si l'on
peut aller du mot codant une tresse au mot codant l'autre tresse en appliquant
les relations d'isotopie.
| Relations |
Illustrations |
| -i,i = i,-i = 0 |
 |
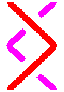 |
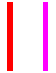 |
| i,j = j,i si |i-j|>1 |
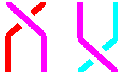 |
 |
. |
| i,j,i = j,i,j si |i-j|=1 |
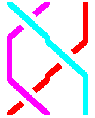 |
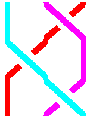 |
. |
Reprenons les exemples précédents en travaillant maintenant
sur les mots.
-
Premier exemple :
1,3,2,-2 -> 1,3 -> 3,1
On a d'abord appliqué la relation i,-i = 0 puis la relation
i,j = j,i.
-
Deuxième exemple :
1,2,1,-2 -> 2,1,2,-2 -> 2,1
On a d'abord appliqué la relation i, j,i = j,i,j puis la relation
i,-i = 0.